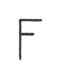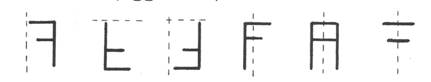Contesti, situazioni, materiali per un apprendimento
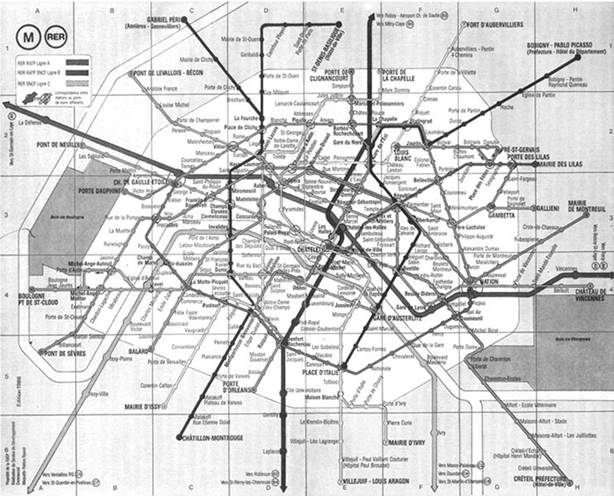
In un viaggio ci sono due aspetti distinti: uno potremmo definirlo "struttura" ed è la mappa spazio-temporale dei luoghi, delle cose, degli spostamenti, l'altro, che potremmo chiamare "processo", è la storia irripetibile del suo accadere. Per sua natura il secondo aspetto appartiene al presente o alla memoria, mentre il primo può anche contemplare la dimensione del futuro, della previsione, del progetto. C'èchi considera il secondo l'essenza stessa del viaggio, e chi lo vive come l'inevitabile insieme degli accidenti che fanno comunque da sfondo al primo. Per un insegnante che voglia guidare un gruppo di alunni nel continente della matematica, c'è sempre la possibilità dei viaggi organizzati, quelli in cui si tenta il più possibile di predeterminare anche il "processo": programmazione, curricoli, unità didattiche e libri di testo sono lì apposta, nell’agenzia scuola. E può partire con la speranza, sostenuta dall’accuratezza dell’organizzazione e dall’affidabilità dell’agenzia, che compagni di viaggio e contesto non gli provochino troppi incidenti o contrattempi. Un'altra possibilità è invece quella del viaggio aperto, d'esplorazione, d'avventura, dove saranno le relazioni (cognitive, affettive..., tra viaggiatori, tra viaggiatori e ambiente...) a determinare, nel presente del suo accadere lo sviluppo del percorso. Nell’ "apprendimento naturale" ciò che spetta alla responsabilità dell’educatore-guida è garantire le condizioni, prima fra tutte l'ascolto, e non lo scegliere i percorsi. Anche un viaggio aperto (e tra viaggio organizzato e viaggio aperto c'è tutta una gradazione) ha una struttura, seppure "leggera": si sceglie una zona da esplorare, si prepara un equipaggiamento, ci si procura una mappa. La mappa delinea una rete di connessioni che la natura o la storia o l'intelletto umano hanno costruito finora tra i luoghi. Una rete che può essere percorsa in molti modi, forse infiniti: la mappa serve dunque a conoscere le possibilità. Chi segue un percorso prestabilito affidandosi a una guida non ha bisogno di una mappa, soprattutto non ha bisogno di usarla, come chi invece il percorso lo costruisce cammin facendo e vuol sapere in ogni momento dove si trova; per non perdersi e per non perdere le occasioni che il territorio gli offre. Ecco la proposta dunque: strutture leggere di apprendimento, mappe di territori matematici, tracce di percorsi possibili nella rete dei concetti, delle nozioni, situazioni pratiche e materiali concreti, problemi e domande stimolo. L'esperienza di scuola ci dà alcuni suggerimenti; per contrasto. Nella scuola, soprattutto dopo l'elementare, normalmente l'apprendimento precede l'applicazione per cui le situazioni problematiche proposte ai bambini (si vedano i problemi dei libri di testo) vengono costruite rivestendo una struttura concettuale astratta (non si sa "astratta" da dove) di elementi presi dalla realtà. Si tratta dunque di situazioni simulate, ma non nel senso proprio di modelli semplificati della realtà, ma di modelli artificiali di un'astrazione. Qui si segue invece il principio didattico che l'apprendimento segue l'operatività e che l'operatività nasce da un problema. Se un problema è tale, se cioè è capace di porre i bambini in ricerca, l'artificiosità o naturalità della situazione perde di importanza. Ciò che più importa è la naturalità con cui il bambino si rapporta alla situazione. Le situazioni proposte sono sempre in qualche modo simulazioni, sia perché per l'appunto sono proposte, cioè vi è un'intenzionalità didattica, sia perché sono ritagliate da un contesto più ampio, sia perché sono semplificate. Quello che importa nel rapporto con la realtà è che da una parte esse siano dentro l’esperienza reale o possibile del bambino, vicino al suo mondo; e dall’altra, se devono "essergli utili nella vita", che per vita non si intenda quella scolastica in cui il metro e il fine dell’utilità è la corrispondenza alla struttura stessa della scuola. È importante ricordare che una mappa può essere considerata come il significante del territorio cui rimanda, ma anche di per sé, come un oggetto con cui entrare in relazione. È sempre possibile che ciascuna delle "mappe" che verranno proposte possa diventare semplice situazione stimolo. Dare ai ragazzi il materiale senza indicazioni di lavoro strutturate vuol dire lasciare che il lavoro parta e si sviluppi dalle domande che i ragazzi pongono di fronte ad esso. È anche vero però che il tipo di materiale, la sua natura e soprattutto la sua struttura, in qualche modo delimitano il campo della ricerca, sia in termini di area concettuale, di "contenuti disciplinari" se si preferisce, sia in termini di abilità, capacità, operatività. Ci sono delle nozioni implicate nell’uso del materiale. "Implicate" significa che emergono alla coscienza e si strutturano nel contesto della soluzione del problema se esso è usato euristicamente come situazione problematica nuova, dove il procedere per tentativi ed errori, l'intuizione, la ristrutturazione di conoscenze precedenti ecc. sono i processi che vengono attivati. La fantasia perversa di un insegnante non dovrebbe avere difficoltà a trovare nuovi problemi, complicando le situazioni o modificando il materiale. Oppure si possono modificare le regole del gioco.. Qui si cercherà di mettere in luce la struttura del materiale, della situazione proposta, che è ciò che lo caratterizza e che lo ha fatto scegliere, sempre con la consapevolezza che la struttura è un fatto cognitivo e che quindi quella è la struttura che emerge alla coscienza di chi scrive stante la sua interazione cognitiva con quel materiale. Non si sottolineerà mai abbastanza, perché ciò è fondamentale nell’ottica non di insegnare ma di facilitare l'apprendimento, che occorre essere attenti ad accogliere la relazione che ogni bambino può costruire con il materiale e che può far emergere una struttura cognitiva diversa inattesa interessante. reti topologiche: IL METRÒ DI PARIGI L'insegnante turista A Parigi per un turista come me il metrò significa poter passare la mattinata a la Villette, accorgersi che è mezzogiorno e arrivare a Beaubourg in tempo per fotografare la fontana di Mirò nell’unica ora in cui il sole a dicembre spunta da dietro la chiesa di St. Merri, tornare in albergo in Rue La Fayette per farsi un sonnellino, ripartire per una visita al Luxembourg e poi di nuovo precipitarsi dall’altra parte al Sacre-Coeur per non perdersi un panorama della città spazzata dagli ultimi raggi di sole sotto un cielo fattosi di neve. A ciò va aggiunta la possibilità di riposare le estremità inferiori messe a dura prova dal vagabondare nel quartiere latino, di ristabilire una normale temperatura corporea dopo una esposizione al vento gelido che striglia la collina di Montmartre, di godersi qualche spezzone di teatro o di musica nelle stazioni, di osservare quale intrico di etnie convivano nella metropoli, di percepire almeno sulla pelle quell’anima della città che un turista di passaggio non può certo pretendere di capire. C'è poi la mia passione per la cartografia che non può essere soddisfatta dall’estensione limitata e dalle sole due linee metropolitane di Milano, ma che si eccitava di fronte all’impresa di decifrare il percorso della mia esplorazione di Parigi. Dunque i pieghevoli che sono a disposizione dei viaggiatori nelle stazioni del metrò e che contengono la mappa della quindicina di linee sotterranee erano al centro della mia attenzione più delle mercanzie sulle bancarelle della riva sinistra: alla fine nella borsa me ne ritrovai una decina; il riaffiorare della mia coscienza professionale mi suggerì di prelevarne altrettanti e così ne ebbi a disposizione giusto uno per ognuno degli alunni che mi attendevano al rientro delle vacanze.
La mappa La mappa naturalmente è a colori: ogni linea del metrò è contraddistinta da un colore. Lungo la linea sono segnate le stazioni, mentre non compare né il tracciato urbano né la toponomastica delle normali piantine cittadine. Accanto c'è l'elenco delle stazioni con l'ubicazione espressa col sistema alfanumerico delle righe e colonne (usato nella "battaglia navale" ma anche in genere nelle cartine stradali). Il problema di chi utilizza il metrò a Parigi è: - Mi trovo a X e devo andare a Y: che percorso fare per arrivarci nel modo più semplice (quali linee prendere, in quale successione, cambiando in quali stazioni)? - Il problema è scomponibile in sottounità: a] verificare se a Y c'è una stazione b] se sì, individuare quali linee vi passano (ogni linea è indicata da un numero che si trova segnato ai due capolinea) c] verificare se a X c'è una stazione d] se sì, individuare quali linee vi passano (vedi b) e] confrontare se vi è una linea che passa sia per X che per Y f] se sì, indicare in quale dei due versi va utilizzata (il verso è indicato con il nome del capolinea di arrivo) g] se no, verificare se vi è qualche stazione in comune tra le linee che passano per X h] se sì, individuare quali spezzoni di linee diverse costituiscono percorsi da X alla stazione comune e da questa a Y (vedi b] ed f]) i] se no, trovare linee che abbiano una stazione in comune con la linea che passa da X e una con quella che passa da Y e poi procedere come in h] j] se i percorsi individuati sono più di uno scegliere quello più economico in termini di spazio-tempo k] per ogni tratto del percorso indicare il verso di percorrenza (vedi f]) e indicare la stazione dove cambiare linea Questo è lo schema totale: la difficoltà di soluzione dipende naturalmente dalla scelta di X e Y e che determina i punti di uscita dallo schema. Vediamo degli esempi. 1) - Mi trovo alla Porte de Versailles e devo andare al Centre Pompidou che si trova a Beaubourg -. La consultazione dell'elenco delle stazioni non riporta la seconda località. Ecco che il problema non è risolvibile senza una cartina più dettagliata in cui compaiano oltre alle denominazioni delle stazioni quelle di tutte le strade. 2) - Mi trovo alla Porte de Versailles e devo andare a Porte de la Chapelle - Entrambe le località sono nell’elenco delle stazioni, che mi dà le coordinate per localizzarle in riquadri sulla mappa. Scopro così che Porte de la Chapelle è il capolinea della linea 12. Da Porte de Versailles passa una linea; per individuarne il numero la seguo fino al capolinea più vicino: scopro così che si tratta della stessa linea 12. La soluzione è dunque - prendo la linea 12 verso Porte de la Chapelle - 3) - Mi trovo a Wagram e devo andare a Saint Maur - Trovate le due stazioni, scopro che stanno sulla stessa linea. Per individuare numero della linea e verso devo proseguire oltre Saint Maur (nel verso di percorrenza Wagram-Saint Maur) fino al capolinea: scopro così che la linea è: - la 3 verso Gallieni - 4) - Mi trovo a Monceau e devo andare a Crimee - A Crimee passa solo una linea; seguendola fino al capolinea più vicino scopro essere la 7. Da Monceau passa solo una linea; seguendola fino al capolinea più vicino scopro essere la 2. Seguendo le due linee scopro che hanno una stazione comune a Stalingrad. Devo dunque prendere la linea 2 da Monceau a Stalingrad e la 7 da Stalingrad a Crimee. Ma devo seguire la 2 oltre Stalingrad fino al capolinea per scoprire il verso in cui devo prendere la 2; lo stesso per la 7. 5) - Mi trovo a Monge e devo andare a Convention - La linea 12, che è l'unica che passa per Conventiion, e la 7 che è l'unica che passa per Monge, non hanno stazioni comuni. Vi sono però linee che hanno stazioni comuni sia con la 12 che con la 7. Ad esempio la 6 (Pasteur e Place d'Italie), la 8 (Madeleine e Opera), la 10 (Sevres Babylonee Jussieu), la 4 (Notre-Dame des Champs e Chatelet). Il percorso più breve sembra - la 7 verso Villejuif fino a Place d'Italie, poi la 6 verso Ch. De Gaulle-Etoile fino a Pasteur, poi la 12 verso Mairie d'Issy fino a Convention - Percorsi anche mentali Le nozioni implicate nel corretto uso della mappa sono essenzialmente quelle attinenti alla geometria topologica. Da un punto di vista topologico la mappa è una rete di linee, o meglio di segmenti, visto che non esistono linee "circolari" e che quindi tutte le linee sono caratterizzate da due capolinea. I punti sulle linee sono di vari tipi: gli estremi (capolinea), gli interni (stazioni dove passa un'unica linea), i nodi a tre (stazioni dove la linea si divide per raggiungere due capolinea diversi come Maison Blanche o dove una linea transita per il capolinea di un'altra, come Gambetta), nodi a quattro (dove si incrociano due linee, come Pigalle), nodi a cinque (dove si incrociano due linee nel capolinea di una terza, come Place d'Italie), nodi a sei (dove si incrociano tre linee, come Bastille), nodi a sette (dove si incrociano tre linee nel capolinea di una quarta, come a Ch. De Gaulle-Etoile), nodi a otto (dove si incrociano quattro linee, come a Montparnasse, oppure si incrociano tre linee dove fanno capolinea altre due, come a Nation). Sono nozioni topologiche il fatto che sulla linea esiste un ordine e quindi un verso di percorrenza, che bastano due punti su una linea aperta per determinare il verso. Gli ultimi due esempi presentati (4 e 5) prima richiedono abilità euristiche e percettive oltre che di rappresentazione spaziale: qual'e la strategia migliore per scoprire se due linee hanno una stazione in comune? Seguirne una (a partire dalla stazione che ci interessa, ma in quale verso?) memorizzando tutte le stazioni, poi ripetere l'operazione sull’altra fino a riconoscere il nome di una stazione già memorizzata; oppure memorizzare il colore di una linea e cercare sull’altra un incrocio con quel colore; oppure "zoomando all’indietro" con una osservazione meno dettagliata cercare di cogliere contemporaneamente lo sviluppo delle due linee e quindi individuarne l'incrocio? L'ultimo esempio (5) richiede in più anche una scelta: allora qual è il criterio di "economia" di un percorso? il numero di stazioni attraversate (e quindi di fermate), il numero di cambi di linea, una somma ponderata di entrambi? Si possono trovare nuovi problemi complicando le situazioni: ad esempio studiare i percorsi più economici di un turista che nel corso di una giornata si vuole recare in più punti determinati della città. Oppure si possono modificare le regole del gioco: il turista dispone di una tessera giornaliera che non consente di utilizzare più di una volta la stessa linea o addirittura di percorrere lo stesso tratto più di una volta. Qualcosa che si avvicina al classico problema topologico dei "ponti di Koenisberg" (o "di Eulero") Con una piccola modifica la mappa può prestarsi ad altri problemi. Per esempio si potrebbe fare delle linee 2 e 6 un'unica linea circolare eliminando il tratto da Ch. De Gaulle-Etoile a Porte Dauphine. Questa linea non avrebbe capolinea. Un primo problema da risolvere sarebbe come individuare i due versi di percorrenza, visto che per andare da una qualsiasi stazione a qualsiasi altra ci sono due percorsi possibili nei due versi (su una linea chiusa occorrono tre punti per definire il verso). Alcuni delle situazioni precedenti possono essere riproposte con questa variante della linea circolare. Altre possibilità..... SOLIDI IMPOSSIBILI
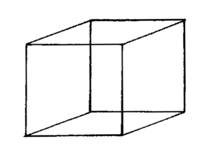
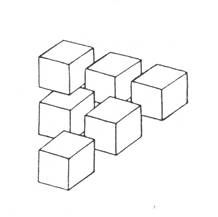
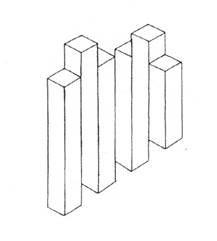
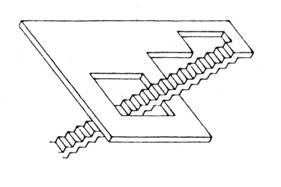
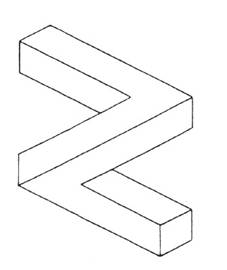
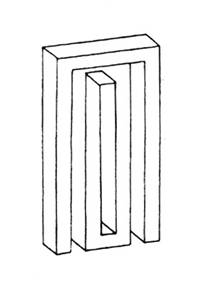
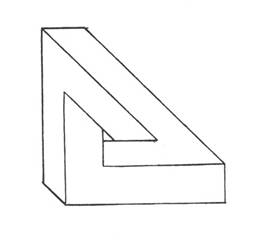
La figura 1 viene definita dalla maggioranza delle persone scolarizzate "un cubo". Una prima pista di ricerca parte dalla proposta "costruiscilo e mettilo in modo che io lo veda come nella figura"; a disposizione: plastilina, cartoncino matita e forbici, filo di ferro. Qualunque sia il materiale scelto e la precisione della costruzione non sarà possibile ottenere un cubo che dia quella immagine. Infatti, se quello della figura 1 è un disegno in prospettiva, allora sicuramente non si tratta di un cubo perché i lati obliqui non potrebbero essere paralleli e quelli trasversali non potrebbero avere tutti uguale lunghezza; se si tratta di una assonometria quello disegnato è un parallelepipedo non cubo essendo i lati rappresentati in obliquo più lunghi degli altri; se si tratta di una immagine proiettiva non si potrebbero vedere i lati posteriori oppure si potrebbero vedere ma in quel caso non si tratterebbe di un cubo (solido) ma dei "lati di un cubo" (un cubo di fil di ferro vuoto); se si tratta di una immagine convenzionalizzata non sono esplicitate le convenzioni; se ... È uno stereotipo scolastico che fa dire che quello "è un cubo". Lo stereotipo agisce a un doppio livello: il primo fa sì che la figura 1 venga ritenuta l'immagine di un cubo nonostante non possieda quelle precise caratteristiche geometriche che lo definiscono. Se nella realtà quotidiana inciampassimo a ogni piè sospinto in cubi di varie dimensioni, materiali e colori, potremmo pensare che l'errore sia di scarsa precisione nel rappresentarli, ma il riferimento esperienziale rispetto ai cubi è proprio il mondo della geometria scolastica dove per l'appunto il cubo è quella entità astratta dotata di quelle precise caratteristiche. Il secondo livello consiste nell’affermare che quello È un cubo e non solo l'immagine di un cubo, sanzionando l'identità del concetto di solido geometrico con la sua rappresentazione bidimensionale e quindi la estraneità del concetto di solido da quello di oggetto reale. Illusione realtà e geometria Nella proposta iniziale, la richiesta di collocare il cubo rispetto al punto di vista apriva il problema della visione: ammettendo per un momento che quello della figura 1 sia un oggetto tridimensionale, fissandolo per un certo tempo, la percezione oscilla tra una visione in scorcio da sopra verso sinistra, e una da sotto verso destra. Anche le altre figure qui riportate vengono accolte come rappresentazioni di oggetti solidi, e solo un’osservazione più attenta rivela che c'è qualcosa che non va. La definizione che viene accettata è quella di solidi "impossibili" o "paradossali". Se ci si prova a chiedere perché questi solidi impossibili sono impossibili, difficilmente la risposta sarà quella corretta: "perché non sono solidi".
La visione è una rappresentazione fisicamente bidimensionale. L'illusione della tridimensionalità si basa su abitudini percettive; quelle per cui ad esempio un uomo visto molto più piccolo è interpretato come più lontano, escludendo per esperienza che sia tanto più piccolo. Si tratta di pre-giudizi percettivi, utili per muoversi nello spazio fisico quotidiano, ma anche a volte pericolosi come dimostra quel campo di fenomeni cui appartengono, come casi estremi, le cosiddette "illusioni ottiche" o molte opere di M.C. Escher. Un’esplorazione di questo campo [1] è una premessa indispensabile a qualsiasi uso di rappresentazioni grafiche di oggetti solidi. Attenzione perché per i ragazzi è affascinante e divertente!
Il problema della scuola è che utilizza per i solidi rappresentazioni prospettiche, spesso imprecise, senza esplicitare, e quindi senza rendere consapevoli, le regole che codificano i rapporti tra queste, gli oggetti tridimensionali e i punti di vista; e questo in un campo, quello della geometria, in cui tali rapporti sono l'essenza stessa della disciplina. Il risultato è che nella scuola non si studia la geometria dei solidi attraverso la loro rappresentazione grafica, si studia la rappresentazione grafica; ma non nel senso del processo che porta dal solido alla sua immagine bidimensionale sul foglio di carta, bensì nel senso dell’oggetto grafico in sé. A dire il vero a scuola ci si occupa di quel processo (prospettiva, proiezioni ortogonali), ma purtroppo ciò avviene in una Materia diversa da quella in cui si studia la geometria dei solidi, perciò non c'è speranza che le conoscenze acquisite nell’una possano essere utilizzate nell’altra. Dunque un lavoro che utilizza i solidi impossibili è un lavoro contro gli stereotipi della scuola, si ispira a Shakespeare (<<Ci sono più cose in cielo e in terra, Orazio, di quante ne immagina la vostra geometria>>) ed è consigliato a giovani supplenti dispettosi. Esso si inserisce a puntino tra due premesse didattiche: la costruzione di modelli e la rappresentazione grafica. Modelli e ombre Un lavoro che si può fare per risolidificare i solidi geometrici è quello di costruirne dei modelli usando materiali plastici. Se il processo di astrazione procede dal meno al più astratto questo è il materiale da usare per primo. Le superfici sono senz’altro più astratte dei solidi visto che non possono esistere senza essere superfici DI qualcosa di solido (esercizio da proporre in proposito: "va in bagno, riempi un lavandino d'acqua, descrivine la superficie e poi portamela"). Le costruzioni con la plastilina, se non si esercitano forme di repressione brutali, danno inevitabilmente vita a forme diciamo non geometriche, e per l'appunto questo può essere una situazione ottimale per capire che cos'è che fa di un oggetto un solido "geometrico", ovvero che nesso c'è tra la geometria dei solidi e la realtà degli oggetti, che è il livello zero del processo di astrazione. Anche costruire modelli delle superfici dei solidi con il cartoncino può essere interessante: oltretutto la differenza tra i due è cruciale per elaborare il concetto di volume come grandezza dello spazio occupato e le procedure per la sua misura (misura non calcolo). Con le superfici il problema che si pone è quello di disegnare su un piano figure che, una volta ritagliate e disposte nello spazio, combacino nei loro lati in modo da costituire le superfici del solido: si tratta di prevedere le forme, le congruenze, i rapporti. Una variante del disegno delle "superfici di sviluppo" può essere quella di proporre il montaggio della superficie del solido a partire dalle facce separate una dall’altra. Per complicare la vita e aguzzare l'ingegno, tra le facce se ne può subdolamente aggiungere qualcuna non necessaria. Terzo grado dell’astrazione sono i lati delle superfici dei solidi. Se ne possono costruire modelli usando del filo di ferro o degli stuzzicadenti infilati in palline di plastilina. Solo a questo punto si avrà qualcosa che assomiglia un po’ di più ai disegni del libro. Le proiezioni ortogonali di figure geometriche sono un classico scolastico, sul quale non è necessario dilungarsi; anche se, stranamente, quasi nessuna classe ha potuto mai vedere davvero una "proiezione" di ombre su tre pareti ortogonali con proiettore disposto perpendicolarmente e magari, prima ancora, disposto in posizioni non regolamentari ma interessanti per capire cosa succede cambiando la relazione spaziale tra oggetto, punto di proiezione e schermo. Un gioco che si può proporre sulle proiezioni è quello di scegliere a casa propria un oggetto semplice e comune, disegnarne le proiezioni sui tre piani ortogonali (magari si può suggerire di guardare davvero l'oggetto da tre direzioni ortogonali, spostandosi attorno ad esso) fare indovinare ai compagni di che oggetto si tratta mostrandone le proiezioni (una sola per volta). Pur di tenere lontani i bambini dai pericoli del contatto con la realtà, di solito a scuola si preferisce far disegnare loro le proiezioni ortogonali a partire dalla rappresentazione assonometrica. Ed è qui che il supplente dispettoso colpisce a tradimento. Con noncuranza egli inserisce tra banali "cubi sormontati da piramidi affiancate da parallelepipedi in bilico su sfere", qualche "solido impossibile". L'effetto migliora se il compito viene dato per casa subito prima della fine della lezione: nel pomeriggio si scatenerà una cascata di telefonate allarmate condite di imprecazioni all’indirizzo del prof. Se la proiezione dei solidi impossibili presenta difficoltà, la loro realizzazione con modelli di cartoncino o filo di ferro è per l'appunto impossibile: come proposta di lavoro è dunque ancora più proficua come generatrice di domande, riflessioni, spunti di lavoro. Può nascere la curiosità di capirci di più in quelle figure. Un suggerimento è quello di cercare individuare nel disegno dove precisamente sta l'incongruenza. Spesso la figura è fatta di parti isolatamente "possibili" e l' "impossibilità" nasce dal loro assemblaggio. Ai ragazzi che ci si appassionano si può proporre di inventare, disegnandoli, altri solidi impossibili. Quelli qui riprodotti vengono da un concorso del genere. LO SPECCHIO E IL DADO Quando un insegnante riesce a ottenere da un alunno una rappresentazione corretta di una configurazione simmetrica, pensa con soddisfazione che, anche grazie alla sua opera didattica, l'alunno abbia scoperto, appreso, applicato un concetto. Forse non ha mai pensato che, prima ancora che venisse a scuola, prima ancora che nascesse, l'organismo di quel bambino aveva già fatto ben di più: si era autoorganizzato sviluppandosi in modo simmetrico (in ciò per la verità non dimostrando superiorità alcuna nei confronti di una aragosta o di un iris). La simmetria sembra essere una delle forme più diffuse e importanti di organizzazione della natura e forse per questo chiunque ne ha una comprensione empatica. Ma pare che la scuola ne voglia anche una consapevolezza a livello di pensiero verbale attraverso la formalizzazione. Ciò non significa che quel primo modo di conoscenza della simmetria debba essere negato, o "superato". Forse si può proprio lavorare su quella consapevolezza che deriva dalla lunga convivenza con il proprio corpo, perché quello della simmetria sia un riconoscimento. Il corpo doppio [2] Un approccio corporeo ha il vantaggio non solo di partire dal vissuto ma anche dallo spazio tridimensionale che è quello fisico. Solo in seguito si arriverà alle figure sul piano: l'astrazione è un processo da seguire, non un oggetto da acquisire. Si può cominciare immaginando che il proprio corpo sia tagliato a metà; ciò significa individuare nel corpo un piano di sezione che lo separi in parti "uguali" (all’inizio si può accettare questa inesattezza). Poi l'indicazione sarà di cercare dei movimenti in cui le due metà si muovano insieme, in modo che in ogni istante la forma che assumono nello spazio le due metà sia uguale. Il piano di sezione immaginario potrà essere indicato da una retta sul pavimento e sul muro. Ai due lati di questo piano possono essere i corpi di due persone a muoversi rispettando le stesse regole: il vantaggio sta nella possibilità di vedere bene il movimento dell’altro, lo svantaggio nel non poter "comandare" contemporaneamente i due movimenti ma, per uno dei due almeno, di dover leggere e imitare un movimento esterno. Naturalmente anziché eseguire movimenti si possono assumere posizioni, il che facilita il controllo. La scoperta che i due movimenti o le due posizioni non sono "uguali" nel senso della congruenza (sovrapponibilità) ma corrispondenti "come le due mani" è più facile nelle posizioni in cui l'orientamento avanti-dietro dei due corpi è parallelo. Se due persone affiancate alzano entrambe la mano destra ci si accorge facilmente che non viene rispettata la regola dell’uniformità rispetto al piano di sezione, mentre se essa viene rispettata le mani alzate non sono identiche. "Simmetria" è allora il nome che viene dato a questa "corrispondenza controlaterale" a modello delle due metà del corpo umano. Camere oscure Nello snodo di passaggio tra spazio tridimensionale e piano si può collocare l'esperienza con la camera oscura [3]. Si prende una scatola da scarpe di cartone. Al centro di una delle facce più piccole si apre un foro di circa un centimetro di diametro sul quale si applicano tre pezzi di nastro adesivo nero posti in modo da delimitare un forellino triangolare di circa un millimetro (foro stenopeico). Al centro della faccia piccola opposta della scatola si apre un foro a forma e grandezza di occhio. Si taglia un pezzo di "carta da lucido" semitrasparente di grandezza uguale alle facce piccole della scatola, se ne piega ad angolo retto una striscia di circa mezzo centimetro che viene incollata non in modo definitivo (esistono colle che si scollano) all’interno del coperchio in modo che, una volta messo il coperchio nella sua posizione usuale, il foglietto di carta penda verticalmente e parallelamente alle facce piccole della scatola. Così la linea che passa dai due fori praticati attraversa perpendicolarmente la carta semitrasparente. Tenendo ben chiusa la scatola e applicando l'occhio all’apposito foro ciò che si vede è l'immagine di ciò che sta davanti alla scatola proiettata sullo schermo di carta semitrasparente. O meglio: lo si vede se l'interno della scatola è perfettamente buio (un accorgimento è di applicare della gomma spugna colorata di nero ai bordi del foro oculare in modo che lo spazio tra il bordo della cavità orbitale e il bordo del foro venga sigillato, impedendo alla luce di entrare da quella parte), se il foro è della grandezza giusta (se è troppo piccolo non entra abbastanza luce, se è troppo grande l'immagine non è nitida), se lo schermo semitrasparente è applicato alla distanza giusta (se è troppo vicino al foro stenopeico l'immagine è troppo piccola, se è troppo vicino al foro oculare è troppo poco luminosa). Queste difficoltà possono diventare occasioni di ricerca. Si può ad esempio portare ai ragazzi una camera oscura già fatta e collaudata e proporre di costruirsene una. Se alle domande "quanto deve essere grande il foro stenopeico?" e "dove deve essere applicato lo schermo?" la risposta sarà "prova!", saranno i ragazzi stessi a scoprire quale influenza hanno queste variabili sul fenomeno. Un altro modo di costruire camere oscure è quello di spostare l'occhio dall’esterno all’interno della scatola. Occorrono scatoloni di cartone più grandi da utilizzare capovolti: lo schermo sarà applicato al fondo, e per poter introdurre la testa si praticheranno dei tagli nei lembi che servono da chiusura in modo che una volta ripiegati resti una apertura delle dimensioni del collo (l'apertura deve essere posizionata in modo che la nuca sia a contatto con la parete opposta al foro stenopeico, altrimenti lo schermo sarà troppo vicino agli occhi rendendo difficoltosa la messa a fuoco) [4]. Ma la cosa più interessante è che i ragazzi, quando hanno in mano (o in testa) una camera oscura perfettamente funzionante e tentano di utilizzarla come "telecamera", non possono fare a meno di incontrare difficoltà nell’inquadratura: l'immagine è capovolta. Specchi Quasi sicuramente saranno i ragazzi stessi a citare le loro esperienze con lo specchio, altrimenti basta chiedere se conoscono qualche altra situazione simile. L'insegnante, per una fortunata combinazione, proprio quel giorno ha nella sua capace borsa uno specchio, e per giunta uno specchio rettangolare senza cornice (e con bordi molati). Si tratta di confrontare l'immagine ottenuta nella camera oscura con quella dello specchio. Per facilitare l'operazione conviene usare un’immagine semplice e senza assi di simmetria: si può ad esempio disegnare in grande una lettera dell’alfabeto come la F (se la si disegna con un pennarello nero su un foglio di carta da lucido la si può vedere anche ribaltando il foglio). Concretamente si può applicare il foglio sul vetro della finestra, osservare la figura attraverso la fotocamera, poi sempre sul vetro o sul banco (l'importante è che si possa agevolmente manovrare intorno ad essa) si può osservare la figura riflessa nello specchio posto perpendicolarmente al piano della figura. Se i ragazzi sono liberi di provare e sono stimolati a farlo, metteranno lo specchio su vari piani tutti perpendicolari a quello della figura ma in varie posizioni ottenendo varie immagini [5]. Le più "normali" sono quelle in cui l'intersezione tra piano dello specchio e piano della figura è disposta lungo i lati del foglio, paralleli quindi agli assi dominanti della F (figg. 2 e 3).
Se le immagini ottenute sono riportate una accanto all’altra su un foglio il risultato è l'evidenza che con lo specchio non si può ottenere l'immagine della fotocamera (fig. 4). Il passo seguente è chiedere ai ragazzi come è possibile ottenerla. Il contesto probabilmente favorirà la direzione dell’esplorazione: se è disponibile più di uno specchio qualcuno arriverà alla soluzione della immagine doppiamente riflessa (in uno specchio si vede riflessa l'immagine della F riflessa da un altro specchio). La trasparenza del foglio di carta da lucido aprirà la possibilità di vedere la figura anche ribaltando il foglio e di scoprire quindi che con un doppio ribaltamento si ottiene la figura della fotocamera, con ribaltamenti singoli (a partire sempre dalla F) quella dello specchio. Uno sviluppo del lavoro è quindi l’esplorazione dell’isomorfismo tra ribaltamento e riflessione speculare. Occorre fare attenzione alle condizioni legate ai modelli materiali che si usano. La carta trasparente come modello del piano è il più vicino al concetto di piano geometrico perché è più facile ignorare la sua terza dimensione. Se come asse di simmetria si sceglie un segmento che attraversa la figura (fig. 5) l'immagine ribaltata (fig. 2) risulta diversa da quella speculare perché lo specchio nasconde una delle due parti e "raddoppia" l'altra (figg. 6 e 7). Maneggiando il foglio con la F non è difficile che si scopra che l'immagine della fotocamera, che sembra il risultato più complicato (doppia trasformazione) si può ottenere anche con una semplice rotazione sul piano di 1/2 giro. Di qui può nascere la richiesta di verificare se anche le altre figure speculari o ribaltate si possono ottenere con rotazioni sul piano. La rotazione di 1/2 giro sul piano appare diversa dal ribaltamento solo perché si è passati alla situazione bidimensionale del piano. Ma il ribaltamento, non come trasformazione geometrica che considera solo gli stati iniziale e finale, ma come movimento nello spazio reale (che è quello che si agisce concretamente lavorando con i modelli), si svolge nello spazio tridimensionale, per cui i due ribaltamenti e la rotazione di 1/2 giro del piano in realtà sono tre rotazioni di 1/2 giro in tre direzioni ortogonali dello spazio. È più facile rendersene conto se si lavora, anziché con una figura su un foglio, con un oggetto che occupa spazio in tutte le direzioni. Il dado è as-tratto Se si cerca un oggetto che facilita l'individuazione di tre direzioni ortogonali e che permette di controllare facilmente i mutamenti di posizione nello spazio, un dado da gioco è ciò che fa al caso. Supponiamo di assumere come spazio di lavoro quello fisico e come direzioni privilegiate quelle dell’osservatore umano [6]; allora avremo una posizione "standard" del dado in cui si distinguono una faccia superiore e una inferiore, e, rispetto all’osservatore, una destra e una sinistra, una anteriore e una posteriore. Assumiamo inoltre come regole del gioco che sono ammessi solo movimenti di rotazione attorno ai tre assi perpendicolari alle facce (si può costruire un dado di plastilina attraversato da tre ferri da lana) che riportino sempre il dado nella posizione standard. Se le facce sono contraddistinte dai segni dei numeri da 1 a 6, ogni stato del dado può essere individuato dall’accoppiamento in una "matrice di stato" dei sei numeri con le sei posizioni delle facce, come ad esempio:
Tra l'altro si può scoprire che, mentre le posizioni relative possono mutare, l'accoppiamento delle facce opposte resta fisso, per cui la matrice può essere semplificata:
Ma allora anche queste informazioni sono sovrabbondanti per descrivere uno stato: infatti se si tengono fisse due facce adiacenti le altre non possono cambiare posizione. Perciò sono sufficienti due facce adiacenti per definire la matrice di stato:
Una prima indicazione può essere quella di scoprire quanti stati diversi ci sono. Si può cercare di calcolarne il numero senza provarli tutti, o comunque individuare una strategia di esplorazione per evitare di dimenticarne qualcuno o di contare due volte lo stesso (per ogni numero su una certa faccia ci sono 4 possibilità ottenute ruotando di 1/4 di giro sull’asse perpendicolare a quella faccia; ci sono 6 numeri che possono comparire su quella faccia...). Ora possiamo limitare i movimenti concessi a rotazioni di 1/2 giro sui tre assi, che chiamiamo ribaltamenti. Sarebbe in questo caso opportuno colorare con la stessa tinta le facce opposte: sono allora consentiti solo i movimenti che riportano lo stesso colore sulla stessa faccia. Gli stati si riducono a 4: siamo nella stessa situazione del foglio con la differenza che quest’ultimo nasconde la terza dimensione. Un gruppo di trasformazioni Finora gli stati, cioè le configurazioni del cubo numerato nello spazio, sono stati considerati come elementi di un insieme, e i movimenti ammessi come passaggi da uno stato all’altro, cioè trasformazioni. Si può passare su un livello diverso di astrazione assumendo come elementi le trasformazioni stesse e operando su di esse. Avremo un insieme di tre trasformazioni: (ribaltamento) ant-pos, sin-des, sup-inf; l'operazione che si può fare utilizzando questi elementi è quella del comporre. È una funzione binaria, cioè a una coppia di elementi (trasformazioni) ne corrisponde uno, mentre le funzioni del livello precedente (trasformazioni) erano unarie, perché a un elemento (stato) ne facevano corrispondere un altro. Il lavoro a questo punto può essere quello di controllare se componendo due trasformazioni, ovvero applicandole di seguito l'una sullo stato risultato dall’altra, si ottiene un’altra trasformazione, cioè si giunge a uno stato che si potrebbe ottenere con un’altra sola trasformazione, compresa tra quelle dell’insieme (verificare gli stati è facile se si usa la matrice di stato). Un’altra caratteristica da esplorare è l'esistenza di trasformazioni inverse di altre, cioè trasformazioni che, se vengono applicate allo stato finale di una trasformazione, riportano allo stato di partenza di quella. Nel nostro caso ogni trasformazione è inversa di se stessa. Ancora si può verificare se l'ordine di composizione di tre trasformazioni è rilevante o meno (associatività: se cioè componendo con la terza quella risultata della composizione delle prime due si ottiene lo stesso risultato che componendo con la prima quella risultata dalla composizione della seconda con la terza. La verifica come sempre si fa applicando le trasformazioni a uno stesso stato iniziale e osservando stati finali (si opera su due livelli logici). Ne viene fuori una tabella come la seguente, nella quale è stata inserita anche una "trasformazione nulla" o "identica", quella cioè che riporta allo stato di partenza (elemento neutro).
Quello che l'insegnante sa, ma che ai ragazzi, impegnati a non perdere il filo della loro esplorazione, interesserebbe ben poco, è che questa è una struttura algebrica di gruppo, il Gruppo di Klein, estremamente interessante (si vedano i lavori di Piaget e di Dienes) perché si ritrova in molte situazioni matematiche e geometriche significative. E questa potrebbe essere un’altra pista.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||