Rappresentazioni grafiche e astrazione

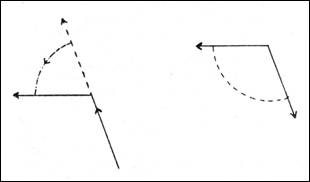
   La rappresentazione grafica in molte situazioni viene utilizzata come passaggio intermedio tra l'esperienza concreta del vissuto e la formalizzazione. Per rappresentazione grafica si intende qualcosa di essenzialmente diverso dal disegno spontaneo: essa è organizzata e spesso realizzata dall’insegnante che ne fornisce il modello ai bambini, e contiene un qualche livello di codificazione. Essa si trova sul cammino non della espressione dell’io soggettivo, ma di una interiorizzazione di significati che dovrebbe costituire un patrimonio di rappresentazioni mentali condivise o almeno confrontabili.

   È questa la direzione di sviluppo dell’apprendimento matematico, che non nega le risonanze affettive e le valenze soggettive che le nozioni possono suscitare in ciascuno, ma che costitutivamente non può rinunciare a una strutturazione di significati comune e univoca; del resto anche lo stesso sviluppo storico della matematica ha portato a una sempre maggiore formalizzazione.

INSIEMI

   Ma la grafica così come è utilizzata nella scuola è davvero una situazione che facilita il passaggio dal vissuto alla rappresentazione astratta? Certamente essa costituisce una prima possibilità di astrazione, nel senso di una "dimenticanza" degli elementi accidentali e una selezione di quelli essenziali al significato, e d'altra parte come astrazione è più accessibile perché gioca su elementi visivi; ma forse sarebbe opportuno analizzare quali elementi vengono dimenticati. L’esame risulta più facile se ci riferiamo a una situazione a tutti nota: la rappresentazione degli insiemi con i diagrammi di Venn.

   Prendiamo come esempio una particolare attività: un bambino, che gioca con i blocchi logici riceve l'indicazione dall’insegnante di "mettere insieme" i triangoli rossi, che si trovano ammucchiati da una parte con i cerchi rossi ammucchiati più in là sul tavolo; il bambino spinge con la mano lungo la superficie del tavolo uno dei mucchi verso l'altro oppure lo prende, lo solleva e lo porta a contatto con l'altro. L'insegnante ora fa disegnare al bambino sul quaderno i triangoli con intorno una linea chiusa, poi più a destra i cerchi all’interno di un’altra linea chiusa e infine ancora più a destra triangoli e cerchi insieme all’interno di un unico "recinto". A questo punto può accadere che l'insegnante aggiunga il segno di unione tra i due primi insiemi e il segno di uguale o una freccia tra il secondo e il terzo.

   Sono qui riconoscibili, come prime forme di astrazione nella rappresentazione grafica, la perdita di "materialità" degli oggetti, la riduzione da tre a due dimensioni con la scelta di una sola faccia, la riduzione delle grandezze, la semplificazione della disposizione spaziale sul piano. La comparsa dei segni costituisce qualcosa di più di una semplificazione: si tratta di una codificazione simbolica, diversa dall'uso delle icone grafiche al posto degli oggetti. Ho l'impressione che ci sia una certa disinvoltura nell’uso del diagramma di Venn, sia per perché si dà per scontato che per i bambini sia "naturale", sia perché non si considerano le implicazioni dell’assunzione di quello che è un codice formale; leggerezza che si può pagare per esempio quando capiterà di voler rappresentare situazioni complesse di intersezioni e inclusioni multiple (classificazioni di figure ecc.).

   Ma se il diagramma di Venn crea problemi come icona perché troppo astratto, altri ne crea come simbolo perché troppo iconico. Il fatto che un segno abbia un certo isomorfismo con ciò che vuole rappresentare può essere un vantaggio per la sua memorizzazione e per la sua facilità d'uso (è il caso della "freccia"), ma può far sorgere difficoltà se il suo "realismo" ostacola la sua generalizzazione concettuale. In altre parole, se il "recinto" sta a rappresentare l'Insieme, e ciò torna estremamente utile per capire ad esempio cos'è un insieme vuoto, come fare per insiemi che non possono stare dentro recinti, come ad esempio "le parole del vocabolario" o "i mestieri"? Dentro i diagrammi di Venn si possono scrivere delle parole, ma poi bisogna pur decidere se quelle sono parole o se rappresentano realtà: in un lavoro sulle relazioni, non si può dire che alla parola "cuoco" serve la pentola o che il mestiere di cuoco termina con la lettera O.

OPERAZIONI

   Ma, tornando al nostro esempio di Unione di Insiemi, vi sono altri e più gravi difficoltà legate all’astrazione come "dimenticanza". Ciò che si perde nella rappresentazione grafica è il contesto e soprattutto l'azione. Per il pensiero concreto del bambino operazione è la propria azione diretta. Se la matematica esige che si passi a operazioni mentali su simboli, lo sviluppo del pensiero esige a sua volta che si rispettino le tappe. L'azione, anche prescindendo dalle dimensioni affettive, dagli aspetti motivazionali, dalla soggettività della percezione, ha comunque una dimensione irriproducibile: il tempo.

   Riguardiamo il disegno sul quaderno: ci sono tre insiemi, contemporaneamente. Mentre nell’azione la creazione dell’Insieme Unione avveniva proprio grazie alla distruzione dell’esistenza separata dei due insiemi, qui accanto all’esistenza attuale dell’Insieme Unione è visibile la memoria dei primi due insiemi; ma senza che nulla indichi la differenza tra la loro natura di fantasmi tornati dal passato e la realtà presente del terzo insieme.

   Quando agli insiemi si sostituiranno i numeri che ne rappresentano le potenze e all’operazione insiemistica di Unione si sostituirà l'Addizione, rimarrà tutta intera la non risolta contraddizione tra ciò che è rappresentato e ciò che si fa, tra il significato di uguaglianza come sostituibilità reciproca e il significato di "risultato" come effetto di un operare che modifica gli stati di partenza.

   Con ciò non sto suggerendo di saltare direttamente dall’azione concreta alla rappresentazione numerica, che poi nella realtà della scuola vorrebbe dire in pratica fare come è sempre stato fatto, cioè eliminare il vissuto dall’apprendimento matematico; sto domandando se la rappresentazione grafica è un passaggio necessario alla concettualizzazione degli insiemi. Le operazioni sugli insiemi sono concrete e nello stesso tempo rappresentabili mentalmente, per cui costituiscono il canale "naturale" verso l'astrazione numerica; credo però sia un errore pensare che (o agire come se) la rappresentazione grafica degli insiemi, così come si usa sui quaderni dei nostri bambini, sia qualcosa di molto vicino all’esperienza vissuta, e credo invece che occorra essere coscienti che si tratta di un livello di astrazione molto più vicino a quello dei numeri.

ORIENTAMENTO

   Ci sono molti altri esempi di usi e abusi scolastici della grafica che creano interferenze con i processi di astrazione, e la geometria, che nella scuola è ancora essenzialmente una scienza basata sulla visione, è quella che ne fa le spese maggiori. Da dove viene l'inestirpabile stereotipo che i triangoli hanno "la punta in alto" e una "base" sola, se non dalla concettualizzazione di un’abitudine a disegnare i triangoli sulla lavagna sempre con un lato orizzontale e in posizione inferiore?

   La geometria affronta essenzialmente due tipi di problemi: i rapporti spaziali di un oggetto con l'ambiente (orientamento) e i rapporti spaziali interni a un oggetto (forme e dimensioni). Il problema dell’orientamento ha come punto di arrivo nell’insegnamento della geometria nella scuola dell’obbligo i sistemi di riferimento polare e cartesiano, utilizzati essenzialmente nella loro rappresentazione grafica sul piano. Il cammino per arrivarci è lungo e le tappe di astrazione progressiva sono molte: dal vissuto globale alla coordinazione degli spazi percettivi, dall’isolamento dello spazio visivo alla sua riduzione a due dimensioni e al piano.

   La dose di astrazione che contiene quest’ultimo passaggio è talmente alta da richiedere una estrema attenzione da parte dell’insegnante. Qui non si tratta di concentrare l'attenzione su una parte della realtà, ma di passare a lavorare su qualcosa che non esiste: può esistere la superficie del mare da sola, senza il mare? È però vero che io posso dire che la superficie del mare è increspata, o che la pianura si estende verso est. È dunque possibile parlare attorno a superfici e alle loro caratteristiche, e questo perché ne esiste una percezione specifica. Ma allora è da questa esperienza percettiva che si deve partire, dalle tracce concrete che l'attività dei bambini scopre o lascia sulle superfici reali. La punta della matita o la "tartaruga" di LOGO non sono altro che la proiezione del soggetto che si muove sul terreno.

   L'uso prematuro della rappresentazione grafica, la quale implica anche inevitabilmente la riduzione in scala e che richiede la sicura consapevolezza degli isomorfismi, rischia di separare l'attività geometrica sul foglio di carta dal suo referente reale, di trasformare l'uso dei sistemi di riferimento in un esercizio difficile che non ha nulla a che fare con l'orientarsi.

   Oltretutto, parlando di orientamento, non si può trascurare il problema dell’orientamento del foglio stesso. Il foglio è un oggetto fisico nello spazio reale ma è anche il piano rappresentato: i due aspetti sono contemporaneamente presenti, ma tra di essi c'è un grande salto di astrazione. Nella sua prima natura il foglio ha un orientamento spaziale, di solito orizzontale sul piano del banco con due assi impliciti, avanti-dietro e sinistra-destra, che si uniformano a quelli del corpo del bambino che su esso agisce, mentre nella sua seconda natura non ha assolutamente un orientamento. Nella geometria euclidea (quella proiettiva e soprattutto quella topologica non possono per loro natura essere ridotte a disegni su un foglio se non in una versione estremamente astratta) la forma è definita dai rapporti interni che non mutano con l'orientamento complessivo rispetto a un sistema di coordinate esterne: l'essenza della geometria euclidea è proprio l'astrazione dal punto di vista.

  Nella scuola l'insegnante disegna sulla lavagna, che ha un orientamento fisico diverso dal foglio dei bambini, e spesso non si preoccupa di "percorrere l'astrazione" per esempio attraverso l'esperienza dello scivolamento del foglio dalla lavagna al banco. Ma il compiere questa operazione non è sufficiente, è solo la condizione necessaria per prendere coscienza delle fondamentale diversità della "situazione lavagna" dalla "situazione banco" in termini di spazio reale: mentre sulla lavagna esiste un'unica direzione verticale e un'unica direzione orizzontale, sul piano del banco non esiste la direzione verticale, che inequivocabilmente è quella definita dalla gravità, ed esistono infinite direzioni orizzontali, altrettanto inequivocabilmente definite come perpendicolari alla verticale. Questi termini si riferiscono allo spazio fisico, tanto è vero che esistono strumenti di verifica basati sulla gravità; ma il filo a piombo e la livella raramente entrano a scuola, forse perché non si sa in quale "Materia" metterli.

   È proprio nella trasformazione operata con il semplice scivolamento del foglio dalla lavagna al banco che è contenuto il grande salto di astrazione dalla proiettiva alla euclidea, da una geometria "della realtà" a uno spazio puramente rappresentato: ciò che rimane invariato nella trasformazione è appunto qualcosa di "assoluto" cioè di non relativo al punto di vista, di slegato dallo spazio fisico.

   Saltando questo passaggio si radica nei bambini l'utilizzo improprio del termine "verticale", per indicare la direzione avanti-dietro del foglio, che sul banco è orizzontale. Il disastro è doppio: da una parte, come ben sa chi lavora nelle scuole professionali per l'edilizia, occorrono sforzi immensi per recuperare una corretta rappresentazione del sistema di riferimento fisico verticale- orizzontale, che pure è quello originale del vissuto; dall’altra altrettanti sforzi, spesso destinati all’insuccesso, devono essere spesi per svincolare i concetti e le operazioni della geometria dall’orientamento fisico di una particolare rappresentazione. Dire che un triangolo disegnato sul banco ha "la punta in su" significa non solo non essere coscienti dell’astrazione euclidea, ma anche non essere padroni della rappresentazione dello spazio fisico.

FORME GEOMETRICHE

   All’intersezione tra l'orientamento e lo studio delle forme sta il concetto di angolo, dove si ripropone il problema della eliminazione della dimensione dell’azione. Il riferimento psicomotorio è qui lo sguardo (semiretta) che cambia direzione, da una di partenza a una di arrivo (lati dell’angolo), quando il corpo ruota attorno al proprio asse (vertice dell’angolo). Un’esperienza che facilita la gradualità dell’astrazione verso il concetto "assoluto" di angolo è quella del controllo dello sguardo mentre si percorre una linea spezzata. Si può passare dal punto di vista soggettivo al trasferimento del sistema di rotazioni del soggetto a un altro punto di vista esterno diversamente orientato (le esperienze con la "tartaruga" di LOGO si inseriscono in questo percorso).

   La rappresentazione grafica pone il problema non tanto della riduzione a due dimensioni quanto della cancellazione del movimento di rotazione di cui restano solo gli stati iniziale e finale, difficilmente riconoscibili come tali. Nell’uso scolastico poi l'angolo è quasi sempre angolo "interno" e ciò richiede, rispetto alla esperienza precedente, un totale ribaltamento percettivo del rapporto tra rotazione e lati dell’angolo (che sono l'unica cosa che si vede nel disegno): mentre quando si percorre una spezzata la rotazione sul vertice avviene tra il prolungamento (sguardo) della direzione precedente e la nuova direzione (lati), l’angolo interno corrisponde alla rotazione che lo sguardo compie se, stando sul vertice, si porta lo sguardo sul secondo lato a partire dal primo (vedi figura). In realtà è una cosa più difficile a dire che a fare, ma appunto occorre farla.

   Oltretutto la dissociazione dell’esperienza della rotazione dalla rappresentazione grafica dell’angolo, ristretta per di più agli angoli interni, crea difficoltà all’apprendimento del concetto di ampiezza e alla sua misura; viene fissato lo stereotipo visivo dell’angolo come "qualcosa a punta" che ne impedisce una corretta generalizzazione agli angoli ottusi e concavi, rari nelle figure geometriche, e a quelli superiori al giro, addirittura non disegnabili.

   L'interferenza delle abitudini scolastiche relative alla rappresentazione delle figure porta a capovolgere l'ordine naturale del processo di astrazione. Non ci sono dubbi che è più facile rappresentare sul foglio un segmento che non un parallepipedo in prospettiva, ma è altresì vero che oggetti a forma di parallelepipedo esistono mentre un segmento non "esiste": al massimo se ne può identificare un modello isolandolo all’interno di una percezione visiva.

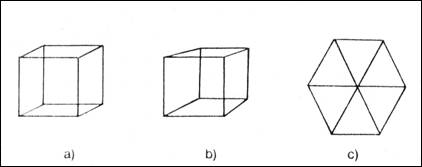
Un bambino che, di fronte ai disegni a) e b), affermi con sicurezza che si tratta di cubi potrebbe venire giudicato dotato di capacità di astrazione e di padronanza dei codici grafici. Quando però lo stesso bambino non riconosce un cubo nel disegno c) e mostra difficoltà a dire quante facce o quanti spigoli ha un cubo, allora nasce qualche sospetto. Alla domanda come possono due figure diverse come a) e b) rappresentare entrambe un cubo e quale delle due assomiglia a come si vede un cubo, il bambino non saprà rispondere, e allora sarà evidente non solo che non ha alcuna consapevolezza dei codici grafici e delle convenzioni che li reggono. Per lui "cubo" è un'associazione stereotipa tra una configurazione gestaltica visiva e una parola; probabilmente non ha mai avuto occasione di osservare dal vero né un cubo pieno, né tanto meno uno fatto dei soli spigoli (ad esempio costruito con del filo di ferro), che è l'unico che può, interposto in un fascio di luce, dare come ombre figure piane del tipo di a) b) e c).

   Un apprendimento rispettoso delle dinamiche di sviluppo dell’astrazione dovrebbe partire dall’esperienza degli oggetti nella loro materialità, prima di "dimenticare" le loro caratteristiche fisiche globali per concentrare l'attenzione sulle loro forme e dimensioni. Si avrebbe così una corretta percezione del volume come grandezza fisica, misurabile cioè con procedimenti fisici, dell’oggetto e non come numero risultante da un calcolo eseguito in base a formule (le chiamano così) pressoché magiche per i bambini. Oltretutto si renderebbe più naturale il passaggio a quell’entità percettivamente vera e materialmente astratta che è la superficie come elemento determinante della forma degli oggetti.

   In un bambino dotato di capacità di astrazione, e quindi di generalizzazione, l'uso prematuro ed esclusivo della grafica in geometria indurrà a pensare che le superfici hanno sempre forme geometriche, che sono sufficientemente piccole da stare in un foglio, che sono sempre piane, che sono associate in qualche modo inesplicabile a due procedure di calcolo, chiamate "area" e "perimetro", difficilissime da distinguere tra loro. La confusione è assicurata dai libri che insistono a chiamare figure piane dei disegni in cui si vede solo la traccia che rimane "percorrendo" con la penna il confine della figura. Ci dev’essere una forte dose di masochismo negli insegnanti: le due nozioni infatti nel vissuto sono completamente distinte. Come l'esperienza del "ricoprire" può introdurre a un operare con le superfici "senza oggetti", così il "percorrere" può far entrare nel mondo di quelle entità ancora più astratte che sono le linee "senza superfici". Pur con le difficoltà date dalla mancanza di "fisicità" sarebbe più facile arrivare a una corretta percezione dell’area e della lunghezza come "grandezze", cioè come qualità caratteristiche, delle superfici e delle linee.

   Ma non basta: sono il ricoprire e il percorrere come attività del soggetto che isolano (svelano, creano?) quelle grandezze dell’oggetto. Ciò significa ricondurre correttamente l'astrazione all’attività del soggetto; e non si tratta di una velleità filosofica, ma di evitare tanti stereotipi deleteri, quelli ad esempio per cui una matita "è lunga" mentre invece "un decimetro cubo pesa un Kilo". Il non pensare alla matita come oggetto anche pesante, o il non specificare di quale linea identificabile all’interno della matita si misura la lunghezza, o il non capire che il decimetro cubo non è un oggetto ma una misura di volume di un oggetto che nel contempo ha anche un peso misurabile, sono effetti della mancanza di quella consapevolezza di fondo nel rapporto tra realtà e rappresentazione matematica che già abbiamo evidenziato nel discorso sul "cubo".

   Al centro dell’uso della grafica sta appunto il nodo della consapevolezza dell’astrazione. Una comprensione dell’astrazione, intesa come specifico concetto astratto, richiede un controllo dell’astrazione, intesa come livello di rappresentazione cui si opera, e questa a sua volta richiede l'esperienza dell’astrazione, intesa come percorso dal vissuto alla formalizzazione.

ELIMINARE LA GRAFICA?

   Senza la consapevolezza della differenza tra la traccia nera di matita sul foglio e la linea geometrica, il bambino sarà portato a pensare che la linea è quella traccia. Questo non è grave per la sua scorrettezza teorica (o meglio non sarebbe grave se poi qualcuno non pretendesse da lui definizioni teoriche), quanto piuttosto per la perdita del rapporto tra esperienza e geometria, tra realtà e sue rappresentazioni, quel rapporto che è così difficile da ricostruire dopo. Eppure l'esperienza spesso è lì "a portata di occhio": quando i bambini osservano il confine tra il mare e il cielo o tra le strisce di colore diverso delle loro maglie, non vedono forse una linea effettivamente a una sola dimensione, come prescrive la teoria?

   Quando, per dare un modello percettivo alla geometria proiettiva, si opera con le ombre non si ha forse davanti agli occhi la concretizzazione della natura della superficie "senza spessore"? C'è come un corto circuito tra esperienza e teoria che tende a saltare la grafica. L'esempio forse più clamoroso è quello della topologia, la prima geometria nello sviluppo del pensiero del bambino e l'ultima nell’evoluzione storica del pensiero matematico. Qui l'esperienza è più vicina alla globalità senso-motoria del vissuto e nello stesso tempo la teorizzazione è più formale: il campo grafico intermedio resta vuoto.

   La geometria moderna ha eliminato la rappresentazione grafica, portando alle estreme conseguenze la formalizzazione, ma ciò può non costituire un argomento decisivo per quanto riguarda l'apprendimento da parte dei bambini. Quello che si può dire però è che forse è tempo di mettere in discussione un ricorso indiscriminato e incontrollato alla grafica.

   Ciò che mi sembra degno di attenzione è oltretutto la dimensione quantitativa del problema: nella misura in cui la scuola fa uso di libri di testo, lavagne, quaderni e fogli da disegno, l'apprendimento passa attraverso la rappresentazione grafica. Anche intendendo in questa sede esclusa dal discorso quella particolare forma di rappresentazione grafica che è la scrittura, il fenomeno è imponente.

   Forse non è possibile né utile eliminare la grafica, ma dovremmo almeno chiederci se il disegno sul quaderno dell’Unione degli Insiemi risponde a una reale necessità di formalizzazione matematica o di apprendimento da parte dei bambini (che gli Insiemi li hanno già uniti) o piuttosto a una esigenza dell’insegnante di documentare (a chi?) il lavoro, e quindi a un suo bisogno di sicurezza.