Informatica conoscenza e realtà
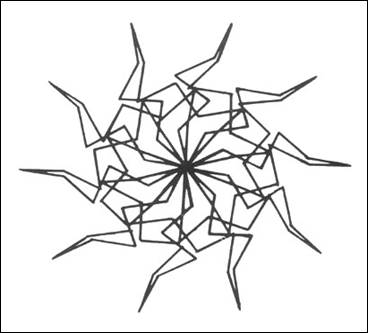
Le impressioni che può suscitare
l’immagini riprodotta qui accanto sono probabilmente diverse e legate al vissuto
personale; sono convinto però che sono ben pochi quelli che le assoceranno
all’informatica. Eppure esse sono state pubblicate da una rivista di
informatica ed elettronica come Chip, proprio perché ottenute con un
computer. UNO
SPECCHIO PER LA MENTE Lo scoprire che si tratta di
rappresentazioni computerizzate di strutture matematiche probabilmente
susciterà in molti un senso di estraneità e di lontananza, oltre che per la
sofisticata tecnologia impiegata, anche per l'inaccessibilità del software,
cioè dei concetti matematici implicati; eppure queste realizzazioni grafiche,
per quanto complesse, hanno alla base un principio molto familiare come il
piano cartesiano (scagli la prima pietra l'insegnante che non conosce la
proverbiale "battaglia navale"). Il piano cartesiano, costituisce un codice
di traduzione tra strutture numeriche e strutture spaziali; una coppia di
numeri corrisponde a un punto; una semplice funzione matematica corrisponde
ad una successione regolare di punti, come una retta o una curva regolare.
Complicando la struttura matematica si complica il disegno, tanto da ricorrere
all’aiuto di un computer, cui viene insegnato il codice di traduzione
numeri-punti (e anche quello numeri-colori, come in questo caso). Ma la cosa interessante di queste figure è
che sono state "commissionate" al computer da un gruppo di
matematici per avere una rappresentazione visiva che facilitasse lo studio di
strutture numeriche complesse difficilmente "immaginabili". Si può
dire dunque che abbiamo davanti delle immagini di cose che esistono solo
nella mente, come appunto le strutture matematiche: in questo senso dunque
parliamo di uno "specchio della mente". Se scendiamo ad un’analisi più
particolare, scopriamo che ogni parte delle figure riprodotte è composta di
parti che ripetono in scala più ridotta la stessa struttura; i livelli di
complessità tuttavia sono tali che il risultato è qualcosa che difficilmente
può essere ricondotto ai nostri stereotipi di disegno geometrico. Probabilmente il fascino di queste
immagini deriva proprio anche da questa combinazione di irregolarità, cioè di
qualcosa che siamo soliti attribuire alla sfera della imprevedibilità
creativa, e di regolarità, che ci riconduce al pensiero razionale. In realtà
l'apparente non-regolarità è determinata dall’aumento della complessità delle
strutture regolari e ciò costituisce un esempio di quell’ipotesi
interpretativa che suggerivamo in un precedente articolo a proposito di ciò
che viene percepito come "automatico" e non [1]. Del resto anche la natura, che spesso
nella cultura della separazione viene o romanticamente ascritta alla sfera
dei sentimenti, della bellezza, della poesia o classicamente assegnata alla
sfera dell’ordine, della razionalità, in realtà fornisce gli esempi più evidenti
di una convivenza indissolubile, prova che l’unità sta sopra e prima delle
separazioni culturali. RICORSIVITÀ
E al mondo della natura appartenevano
quegli oggetti che, facendo sfacciata mostra di sé su una bancarella del mercato
di Campo dei Fiori a Roma, sono stati la causa scatenante di queste
riflessioni. Sono un appassionato di fotografia con un'attenzione particolare
per le geometrie della natura che a volte sfiora la mania, ma i miei
interessi culinari finiscono per delimitare il campo delle conoscenze, e poi
a Milano sono più diffusi i cavolfiori; insomma la scoperta della struttura
ricorsiva dei broccoli fu per me una vera folgorazione. E poiché la
ricorsività è uno degli argomenti più interessanti che affronto nei corsi di
alfabetizzazione informatica (in particolare su LOGO), la coincidenza non
poteva lasciarmi indifferente. Il modulo che contiene sé stesso è una
struttura affascinante per menti un tantino paranoiche, ma è qualcosa che si
ritrova anche nelle più famigliari filastrocche come: C'era una volta un re, seduto sul sofà, che disse alla sua serva: -raccontami una storia-. La serva incominciò: C'era una volta un re, seduto sul sofà, che disse alla sua serva: -raccontami una storia-. La serva incominciò: C'era
una volta un re...
È nella stessa natura delle cose, o del pensiero umano, il fatto che a
volte si creino queste situazioni "a specchi contrapposti", che
sono l'immagine più viva dell’"infinito": [...] Diaz passò tutta la sera senza dire
una parola, tirandosi indietro il ciuffo bianco e andò avanti così fino a
quando, dopo cena, si infilò uno stuzzicadenti in bocca e disse:
"Constante li tira sulla destra".
"Sempre", fece il presidente del club
"Però lui sa che io so"
"E allora siamo fregati"
"Si, però anch’io so che lui sa", disse ‘el gato’
"Quindi tuffati sulla sinistra ed è fatta", fece uno di
quelli che erano seduti a tavola "No, lui sa che io so che lui
sa", disse ‘el gato’ Diaz e si alzò per andare a dormire. [2] Per uscire dall’anello senza fine, occorre
che il modulo riproduca sé stesso ma con una variazione, che può essere
semplicemente quella della dimensione. Ed ecco le proverbiali quanto
misteriose "scatole cinesi", o le più familiari
"matrioske", le bambole di legno russe inserite una nell’altra. Non sempre i moduli stanno uno dentro
l'altro: in alcuni molluschi gasteropodi è l'originarsi dell’uno dall’altro
che si rende visibile in una conchiglia. Anche nell’essenza stessa della natura, a
livello di quelle particelle elementari che ne costituiscono la base fisica
universale, ritroviamo una forma di ricorsività [3]. Un
elettrone in movimento emette e riassorbe fotoni "virtuali" (creati
e annichilati prima che possano essere visti); un fotone a sua volta può
decadere, per un brevissimo istante, in coppie elettrone- positrone
(anti-elettrone); questi ultimi si annichilano reciprocamente facendo ricomparire
un fotone, ma prima l'elettrone può emettere un fotone e così via. La propagazione
di un elettrone è accompagnata dunque da una nuvola di particelle virtuali
che si creano ricorsivamente una dall’altra.
Gli esempi fatti si riferiscono ad ambiti molto diversi, ma tutti sono
stati descritti utilizzando quello strumento ricorsivo che è il linguaggio
verbale. La possibilità di inserire in un enunciato un argomento costituito
da un enunciato e così via (nei limiti della capacita del ricevente di tenere
in sospeso la comprensione dell’enunciato di ordine superiore fino alla
chiusura di tutti quelli inferiori) è molto sfruttata dalla lingua tedesca.
Anche in italiano la costruzione è usuale: l'esempio dantesco (Paolo e
Francesca), con i suoi primi due versi a tripla inclusione è unico solo per
fama poetica Amor, ch'a nullo amato amar perdona, mi prese del costui piacer sì forte che,
come vedi, ancor non m'abbandona.
A
questo punto non sembrerà strano ritrovare ricorsività anche in altre
espressioni della cultura umana: nel linguaggio della pittura, come in molte
xilografie di M.C. Escher, o del cinema. Nel film "Lo stato delle
cose", del regista tedesco Wim Wenders, il protagonista Frederick è il regista
di una troupe cinematografica che sta girando un film di ambientazione
fantascientifica (che è tra l'altro un remake di un film "vero"):
nella scena iniziale del film di Wenders (I livello) si vede appunto una scena
di questo film, girato dalla troupe di Frederick (II livello), ed in
essa uno dei personaggi usa una cinepresa (III livello). Anche nella musica si ritrovano strutture
ricorsive: la Sinfonia n.2 di S. Rachmaninov e il Concerto per
pianoforte n.5 di Prokof’ev contengono cicli di scale con tempi diversi;
il Canone per Tonos dell’ "Offerta musicale" di J.S. Bach ha
una struttura modulare in cui ogni ciclo ha un finale che si riconnette
all’inizio ma con un cambio di tonalità, finché dopo sei di queste
modulazioni ci si ritrova al punto di partenza un'ottava sopra. Un altro
esempio è quello, forse più familiare, del "Bolero" di Ravel.
PENSARE
FIGURE E DISEGNARE PENSIERI
Tornando alle nostre immagini computerizzate iniziali, viene facile
pensare che dal punto di vista della struttura si tratti di cose per
matematici professionisti. La figura qui riprodotta sicuramente si colloca
qualche gradino più in basso nella scala della complessità, tuttavia si
direbbe ancora inaccessibile ai comuni mortali da un punto di vista
strutturale. Per disegnarla è stato usato un computer che utilizza il
linguaggio LOGO: una punta (la "tartaruga"), luminosa sullo schermo
o grafica sulla carta, traccia un percorso seguendo una sequenza di
istruzioni. La "procedura" per ottenere la figura è la seguente: PER RUOTA ASSEGNA "LATO 30 ASSEGNA "ANGOLO 6 ASSEGNA "INCREMENTOLATO 0 ASSEGNA "INCREMENTOANGOLO 210 SPIRA :LATO :ANGOLO :INCREMENTOLATO
:INCREMENTOANGOLO FINE PER SPIRA :LATO :ANGOLO :INCREMENTOLATO
:INCREMENTOANGOLO AVANTI :LATO DESTRA :ANGOLO SPIRA :LATO + :INCREMENTOLATO :ANGOLO +
:INCREMENTOANGOLO :INCREMENTOLATO :INCREMENTOANGOLO FINE È comprensibile il disagio di molti di
fronte ad un messaggio in un linguaggio diverso da quello naturale, ma si può
constatare che si tratta comunque di poche righe e con parole riconoscibili.
Piuttosto, anche per chi conosce il
linguaggio, è ancora forse troppo difficile ritrovare nel disegno prodotto
una rappresentazione di quella struttura ricorsiva che la procedura
suggerisce. Questa
volta però non è necessario scendere di più lungo la scala della complessità
per cominciare a controllare questo isomorfismo. Con la stessa procedura,
semplicemente assegnando valori numerici diversi alle variabili (si tratta di
quegli "ASSEGNA" della prima parte), si costruisce una semplice
spirale triangolare. A questo punto è molto più facile leggere la procedura
come una descrizione della struttura della figura: essa infatti è il disegno
del confine di un triangolo che non si chiude mai perché ogni volta il lato diventa
più lungo. Infatti la procedura SPIRA (che utilizza le quattro variabili
LATO, ANGOLO, INCREMENTOLATO, INCREMENTOANGOLO) consiste in un tratto
rettilineo (AVANTI :LATO) e in un angolo (DESTRA :ANGOLO), seguiti dalla
ripetizione della procedura stessa (SPIRA) in cui però viene inserito un
incremento del lato (:LATO + :INCREMENTOLATO) e un incremento dell’angolo
(che in questo caso è nullo): la procedura, come le "scatole
cinesi", contiene se stessa, ma con una variazione di grandezza ogni
volta,. Si comincia qui forse ad intravedere che
cosa abbia tutto ciò a che fare con lo sviluppo delle attività cognitive e
l'educazione dei bambini. EPISTEMOLOGIA
ED EURISTICA Un bambino, soprattutto nella scuola
elementare, difficilmente è in grado di costruire da sé quella procedura, ma
ciò che può già fare è cominciare a manipolarla. Si può ad esempio chiedergli
come modificarla per ottenere una spira quadrata. Se ha fatto un minimo di
esperienza con la "tartaruga" di LOGO, costruendo le figure del
quadrato e del triangolo anche solo con le istruzioni AVANTI e DESTRA, non
avrà molta difficoltà ad individuare il valore dell’angolo come l'elemento da
modificare. Il computer fa sì che la verifica della correttezza dell’ipotesi
sia immediata e visibile: sullo schermo apparirà una spirale quadrata. Quello
che il bambino vede è in fondo l'immagine visiva di quella sua ipotesi. Esempi ancora più semplici di questo
discorso si trovano nella pratica ormai "tradizionale" di uso del
linguaggio LOGO con i bambini. Quando un bambino scopre che dando successivamente
delle istruzioni alla "tartaruga" ottiene il disegno di un quadrato
ha sperimentato quella operazione mentale di "assemblaggio" che
consiste nel costruire un’unità più complessa mettendo in un rapporto di ordine
sequenziale unità più piccole. Questa linea di discorso va nella
direzione dello sviluppo della capacità euristica, intesa come l'arte di
trovare la soluzione ai problemi, e in generale di quella che Papert, il
matematico-informatico padre di LOGO e allievo di Piaget, ha chiamato la
ricerca epistemologica dei bambini, cioè la costruzione della consapevolezza
del modo di funzionare del proprio pensiero.
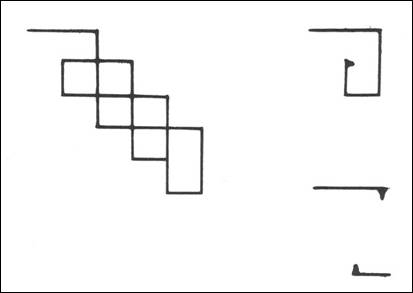
Se si chiede ai ragazzi di far eseguire
come percorso alla tartaruga di LOGO il disegno della figura qui accanto le
soluzioni possibili sono tante; la ricerca di soluzioni "economiche"
o "furbe" o "eleganti" o "veloci" è una ricerca
sul pensiero, perché si tratta di individuare le strutture in cui il pensiero
organizza la realtà che percepisce o i propri processi costruttivi. Di questo
si tratta quando il ragazzo scopre che in quel disegno è nascosto un
"modulo", cioè un disegno più semplice ripetuto. E non basta: lo
stesso modulo può essere descritto come l'assemblaggio di due unità di
percorso, ciascuna descrivibile come ripetizione di un modulo ancora più semplice. È la scoperta che una struttura può
contenere altre strutture e la conquista di un livello superiore di
organizzazione, ben oltre l'ordine sequenziale. E ancora una volta LOGO fa da
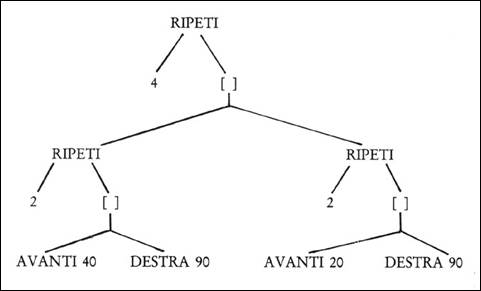
specchio per la mente, perché la procedura per il disegno evidenzia proprio
questa strutturazione: la figura seguente è una rappresentazione grafica
della struttura in LOGO).
Soffermiamoci un momento su questa figura
"a radici": è la stessa che si ritrova nella teoria della lingua di
Parisi; anch’essa ha alla base una relazione predicato-argomento che si
articola ricorsivamente a vari livelli, dal significato della singola parola
all’enunciato, al testo intero. RIPETERE, nel modello linguistico di
Parisi, è un predicato a tre argomenti, "chi", "che cosa"
e "quante volte". In LOGO, RIPETI è un operatore che opera su due
oggetti "quante volte" e "che cosa". Rispetto al modello
linguistico manca il primo argomento, ma ciò è dovuto alla forma imperativa,
la cui struttura completa sarebbe "io ordino a qualcuno che questo
qualcuno ripeta qualcosa un certo numero di volte"; poiché la
comunicazione con la macchina ha sempre questa forma e poiché il
"qualcuno" è sempre la macchina (o meglio l’"automa LOGO")
viene sempre sottintesa la parte superiore della struttura e il primo
argomento, cioè "io ordino alla macchina che la macchina...".
Questo apre una strada interessante nel campo della ricerca sulla lingua in cui
LOGO potrebbe giocare un suo ruolo e che varrebbe la pena di esplorare.
Euristica è anche capacità di riconoscere
e di ricostruire strutture come queste, sia in fase di analisi che di costruzione.
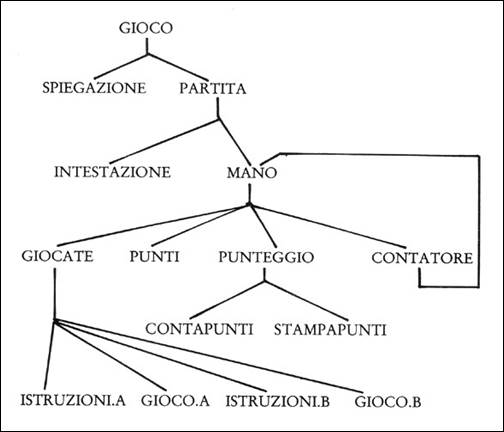
La realizzazione al computer di un progetto come quello di un piccolo gioco
di simulazione richiede ai ragazzi una prima fase di lavoro di analisi strutturale:
la figura accanto è un esempio di diagramma a radici che rappresenta il
progetto nei suoi successivi livelli di dettaglio: le unità al livello più
basso sono poi quelle che i ragazzi, divisi in gruppetti, hanno dovuto
realizzare come procedure in linguaggio LOGO. INSEGNARE
PER IMPARARE La possibilità di analizzare la struttura
di un procedimento ha un ruolo essenziale anche nell’apprendimento delle
conoscenze di base, come le operazioni aritmetiche. Quando un bimbo chiede
all’insegnante "se moltiplicare vuol dire ripetere più volte un numero,
perché 3 x 0 fa 0?" oppure se un ragazzo particolarmente diligente,
seguendo le istruzioni del libro di testo, che gli dicono che "4 alla
seconda" significa "4 moltiplicato per sé stesso due volte"
scrive giustamente "4 x 4 x 4" e poi chiede perché non va bene il
risultato, c'è proprio bisogno di un'analisi delle procedure per rendere
chiari i concetti. Nel caso della moltiplicazione la
procedura consiste nella ripetizione per un determinato numero di volte della
azione di un operatore additivo applicato a partire dallo 0. Nel caso della potenza
la ripetizione riguarda un operatore moltiplicativo a partire dall’unità (1 X
4 X 4). È proprio lo stato iniziale che viene elegantemente dimenticato
generando così contraddizioni o legittime incomprensioni (naturalmente per
capire perché lo stato iniziale nel caso della potenza è l'unità occorre
avere già acquisito l'operazione concreta del raggruppare di cui la potenza è
la rappresentazione numerica). Naturalmente per fornire ai bambini
spiegazioni di questo tipo sarebbe sufficiente la lavagna, ma, a parte il
discorso della maggiore popolarità che riscuote il computer rispetto
all’insegnante di matematica, la cosa cambia completamente quando si chiede
ai bambini di insegnare loro la moltiplicazione al computer, scrivendo la
procedura necessaria; tecnicamente la cosa non è poi così difficile purché si
abbia chiaro il procedimento. Sembra un circolo vizioso: se il bambino
conoscesse già il procedimento non ci sarebbe bisogno di usare il computer
per farglielo imparare. In realtà è un circolo vizioso solo in una concezione
passiva dell’apprendimento; per il bambino l'attività dell’insegnare (a
quell’ignorante dell’automa LOGO) è molto più motivante, tanto da poter
costituire l'innesco del processo di apprendimento, ma soprattutto è appunto
un’attività, non un memorizzare passivo. Nell’esempio di prima, per insegnare
a LOGO una procedura ricorsiva come quella della potenza è necessario
esplicitare la situazione di partenza e ciò costringe a non dimenticare
quell’"1" tanto importante e misconosciuto. Il discorso non vale solo per i bambini.
L'abitudine alla routine, da vecchi "Aristogitoni", sovrapposta ad
una formazione professionale (parlo della professione di educare o anche solo
di insegnare), che nel caso degli insegnanti medi semplicemente non esiste a
livello istituzionale, porta spesso a non analizzare a fondo quelle
conoscenze, quelle operatività che pretendiamo che i bambini imparino. Tanto
che si accolgono con dispetto o addirittura si ignorano le contraddizioni che
emergono. Ebbene, il computer è così poco "intelligente" che
insegnare ad esso diventa un utile forma di addestramento professionale ad
esplicitare concetti e procedimenti, senza dare nulla per scontato e senza
approssimazioni facilone. L'utilità di avere qualcosa in cui
specchiare il proprio pensiero ci conduce dunque alla morale di questo discorso:
un buon insegnante, se proprio non se la sente di usare LOGO, dovrebbe almeno
frequentare di più le bancarelle dei mercati e cucinare più spesso i
broccoli. |